
X - is the mean of all the x -values, y - is the mean of all the y -values, and n is the number of pairs in the data set. Where S S x x = Σ x 2 − 1 n ( Σ x ) 2, S S x y = Σ x y − 1 n ( Σ x ) ( Σ y ) Its slope β ^ 1 and y -intercept β ^ 0 are computed using the formulas β ^ 1 = S S x y S S x x a n d β ^ 0 = y - − β ^ 1 x. It is called the least squares regression line The line that best fits a set of sample data in the sense of minimizing the sum of the squared errors. Given a collection of pairs ( x, y ) of numbers (in which not all the x -values are the same), there is a line y ^ = β ^ 1 x + β ^ 0 that best fits the data in the sense of minimizing the sum of the squared errors. The idea for measuring the goodness of fit of a straight line to data is illustrated in Figure 10.6 "Plot of the Five-Point Data and the Line ", in which the graph of the line y ^ = 1 2 x − 1 has been superimposed on the scatter plot for the sample data set. The line y ^ = 1 2 x − 1 was selected as one that seems to fit the data reasonably well. We will do this with all lines approximating data sets. We will write the equation of this line as y ^ = 1 2 x − 1 with an accent on the y to indicate that the y-values computed using this equation are not from the data. (which will be used as a running example for the next three sections).
#The slope of the simple linear regression equation how to
We will explain how to measure how well a straight line fits a collection of points by examining how well the line y = 1 2 x − 1 fits the data set x 2 2 6 8 10 y 0 1 2 3 3 Once the scatter diagram of the data has been drawn and the model assumptions described in the previous sections at least visually verified (and perhaps the correlation coefficient r computed to quantitatively verify the linear trend), the next step in the analysis is to find the straight line that best fits the data.
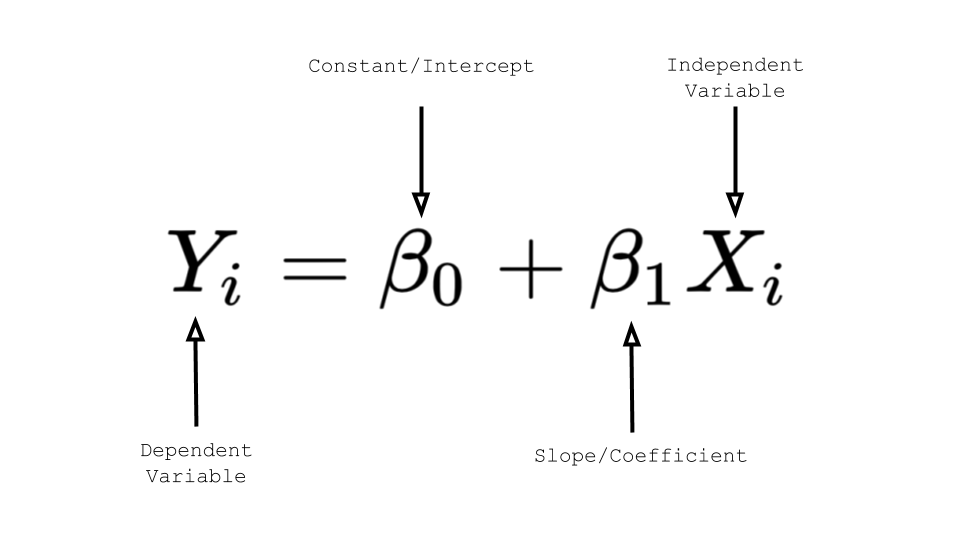
Goodness of Fit of a Straight Line to Data


 0 kommentar(er)
0 kommentar(er)
